Все правила по треугольникам. Виды треугольников, углы и стороны
Типы треугольников
Рассмотрим три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки (рис. 1).
Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков (три точки, не лежащие на одной прямой) – вершинами треугольника.


В таблице 1 перечислены все возможные типы треугольников в зависимости от величины их углов .
Таблица 1 – Типы треугольников в зависимости от величины углов
| Рисунок | Тип треугольника | Определение |
 | Остроугольный треугольник | Треугольник, у которого все углы острые , называют остроугольным |
 | Прямоугольный треугольник | Треугольник, у которого один из углов прямой , называют прямоугольным |
 | Тупоугольный треугольник | Треугольник, у которого один из углов тупой , называют тупоугольным |
| Остроугольный треугольник |
 Определение: Треугольник, у которого все углы острые , называют остроугольным |
| Прямоугольный треугольник |
 Определение: Треугольник, у которого один из углов прямой , называют прямоугольным |
| Тупоугольный треугольник |
 Определение: Треугольник, у которого один из углов тупой , называют тупоугольным |
В зависимости от длин сторон выделяют два важных типа треугольников.
Таблица 2 – Равнобедренный и равносторонний треугольники
| Рисунок | Тип треугольника | Определение |
 | Равнобедренный треугольник | боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника |
 | Равносторонний (правильный) треугольник | Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
| Равнобедренный треугольник |
 Определение: Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника |
| Равносторонний (правильный) треугольник |
 Определение: Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
Признаки равенства треугольников
Треугольники называют равными , если их можно совместить наложением .
В таблице 3 приведены признаки равенства треугольников .
Таблица 3 – Признаки равенства треугольников
| Рисунок | Название признака | Формулировка признака |
 | по двум сторонам и углу между ними | |
 | Признак равенства треугольников по стороне и двум прилежащим к ней углам | |
 | Признак равенства треугольников по трём сторонам |
| Признак равенства треугольников по двум сторонам и углу между ними |
|
| Формулировка признака
. Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны |
| Признак равенства треугольников по стороне и двум прилежащим к ней углам |
|
| Формулировка признака
. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны |
| Признак равенства треугольников по трём сторонам |
|
| Формулировка признака
. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны |
Признаки равенства прямоугольных треугольников
Для сторон прямоугольных треугольников принято использовать следующие названия.
Гипотенузой называют сторону прямоугольного треугольника, лежащую против прямого угла (рис. 2), две другие стороны называют катетами .
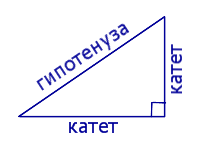
Таблица 4 – Признаки равенства прямоугольных треугольников
| Рисунок | Название признака | Формулировка признака |
 | по двум катетам | |
 | Признак равенства прямоугольных треугольников по катету и прилежащему острому углу | |
 | Признак равенства прямоугольных треугольников по катету и противолежащему острому углу | Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
 | Признак равенства прямоугольных треугольников по гипотенузе и острому углу | Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
 | Признак равенства прямоугольных треугольников по катету и гипотенузе | Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по двум катетам |
|
| Формулировка признака
. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по катету и прилежащему острому углу |
|
| Формулировка признака
. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по катету и противолежащему острому углу |
Стандартные обозначения
Треугольник с вершинами A , B и C обозначается как (см. рис.). Треугольник имеет три стороны:
Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):
Треугольник имеет следующие углы:
Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).
Признаки равенства треугольников
Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:
- a, b, γ (равенство по двум сторонам и углу лежащему между ними);
- a, β, γ (равенство по стороне и двум прилежащим углам);
- a, b, c (равенство по трём сторонам).
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
Некоторые точки в треугольнике - «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли . Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это - точки Аполлония . Точки и такие, что и называются точками Брокара .
Прямые
В любом треугольнике центр тяжести, ортоцентр и центр описанной окружности лежат на одной прямой, называемой прямой Эйлера .
Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара . На ней лежат точки Аполлония. Также на одной прямой лежат точки Торричелли и точка Лемуана. Основания внешних биссектрис углов треугольника лежат на одной прямой, называемой осью внешних биссектрис . На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью , она перпендикулярна прямой Эйлера.
Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек перпендикулярны.
Треугольники
- Треугольник с вершинами в основаниях чевиан, проведённых через данную точку, называется чевианным треугольником этой точки.
- Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.
- Треугольник в вершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником . Окружностно-чевианный треугольник подобен подерному.
Окружности
- Вписанная окружность - окружность , касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром .
- Описанная окружность - окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.
- Вневписанная окружность - окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их радикальный центр - центр вписанной окружности срединного треугольника, называемый точкой Шпикера .
Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера . Центр окружности девяти точек лежит на прямой Эйлера. Окружность девяти точек касается вписанной окружности и трёх вневписанных. Точка касания вписанной окружности и окружности девяти точек называется точкой Фейербаха . Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, ортезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности - окружности Конвея . В любой треугольник можно вписать три окружности таким образом, что каждая из них касается двух сторон треугольника и двух других окружностей. Такие окружности называются окружностями Мальфатти . Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна .
В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера . Отрезки, соединяющие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера . Она служит центром гомотетии , которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.
Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна , а отрезки, соединяющие вершины с точками касания вневписанных окружностей - в точке Нагеля .
Эллипсы, параболы и гиперболы

Вписанная коника (эллипс) и её перспектор
В треугольник можно вписать бесконечно много коник (эллипсов , парабол или гипербол). Если в треугольник вписать произвольную конику и соединить точки касания с противоположными вершинами, то получившиеся прямые пересекутся в одной точке, называемой перспектором коники. Для любой точки плоскости, не лежащей на стороне или на её продолжении существует вписанная коника с перспектором в этой точке.

Описанный эллипс Штейнера и чевианы, проходящие через его фокусы
В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника). Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера . Если аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера.

Эллипс Брокара и его перспектор - точка Лемуана
Эллипс с фокусами в точках Брокара называется эллипсом Брокара . Его перспектором служит точка Лемуана.

Свойства вписанной параболы

Парабола Киперта
Перспекторы вписанных парабол лежат на описанном эллипсе Штейнера. Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр. Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта . Её перспектор - четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера .

Гипербола Киперта
Если описанная гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны). Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек.
Преобразования
Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны). Изогонально сопряжёнными являются многие пары замечательных точек : центр описанной окружности и ортоцентр, центроид и точка Лемуана, точки Брокара. Точки Аполлония изогонально сопряжены точкам Торричелли, а центр вписанной окружности изогонально сопряжён сам себе. Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники - в прямые. Так, изогонально сопряжены гипербола Киперта и ось Брокара, гипербола Енжабека и прямая Эйлера, гипербола Фейербаха и линия центров вписанной о описанной окружностей. Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают. Фокусы вписанных эллипсов изогонально сопряжены.
Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением . Оно также переводит прямые в описанные коники. Изотомически сопряжены точки Жергонна и Нагеля. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.
Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием . Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция - проективное преобразование , которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.
Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной полярой исходной точки. Ортоцентрическая ось - трилинейная поляра ортоцентра; трилинейной полярой центра вписанной окружности служит ось внешних биссектрис. Трилинейные поляры точек, лежищих на описанной конике, пересекаются в одной точке (для описанной окружности это точка Лемуана, для описанного эллипса Штейнера - центроид). Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности (если точка, изогонально (изотомически) сопряжённая точке , лежит на трилинейной поляре точки , то трилинейная поляра точки, изогонально (изотомически) сопряжённой точке лежит на трилинейной поляре точки ).
Кубики
Соотношения в треугольнике
Примечание: в данном разделе , , - это длины трёх сторон треугольника, и , , - это углы, лежащие соответственно напротив этих трёх сторон (противолежащие углы).
Неравенство треугольника
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном - равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:
Неравенство треугольника является одной из аксиом метрики .
Теорема о сумме углов треугольника
Теорема синусов
,где R - радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a < b < c, то α < β < γ.
Теорема косинусов
Теорема тангенсов
Прочие соотношения
Метрические соотношения в треугольнике приведены для :
Решение треугольников
Вычисление неизвестных сторон и углов треугольника, исходя из известных, исторически получило название «решения треугольников» . При этом используются приведенные выше общие тригонометрические теоремы.
Площадь треугольника
Частные случаи ОбозначенияДля площади справедливы неравенства:
Вычисление площади треугольника в пространстве с помощью векторов
Пусть вершины треугольника находятся в точках , , .
Введём вектор площади . Длина этого вектора равна площади треугольника, а направлен он по нормали к плоскости треугольника:
Положим , где , , - проекции треугольника на координатные плоскости. При этом
и аналогично
Площадь треугольника равна .
Альтернативой служит вычисление длин сторон (по теореме Пифагора) и далее по формуле Герона .
Теоремы о треугольниках
Теорема Дезарга : если два треугольника перспективны (прямые, проходящие через соответственные вершины треугольников, пересекаются в одной точке), то их соответственные стороны пересекаются на одной прямой.
Теорема Сонда́ : если два треугольника перспективны и ортологичны (перпендикуляры, опущенные из вершин одного треугольника на стороны, противоположные соответственным вершинам треугольника, и наоборот), то оба центра ортологии (точки пересечения этих перпендикуляров) и центр перспективы лежат на одной прямой, перпендикулярной оси перспективы (прямой из теоремы Дезарга).
Деление треугольников на остроугольные, прямоугольные и тупоугольные. Классификация по соотношению сторон делит треугольники на разносторонние, равносторонние и равнобедренные. Причем каждый треугольник одновременно принадлежит к двум . Например, он может быть прямоугольным и разносторонним одновременно.
Определяя вид по типу углов, очень внимательны. Тупоугольным будет называться такой треугольник, у которого один из углов является , то есть составляет боле 90 градусов. Прямоугольный треугольник может быть вычислен по наличию одного прямого (равного 90 градусам) угла. Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла острыми.
Определяя вид треугольника по соотношению сторон, для начала вам придется узнать длины всех трех сторон. Однако если по условию длины сторон вам не даны, помочь вам смогут углы. Разносторонним будет являться треугольник, все три стороны которого имеют разную длину. Если длины сторон неизвестны, то треугольник может быть классифицирован как разносторонний в случае, если все три его угла являются разными. Разносторонний треугольник может быть тупоугольным, прямоугольным и остроугольным.
Равнобедренным будет являться треугольник, две из трех сторон которого равны между собой. Если длины сторон вам не даны, ориентируйтесь по двум равным между собой углам. Равнобедренный треугольник, как и разносторонний, может быть и тупоугольным, и прямоугольным и остроугольным.
Равносторонним может быть только такой треугольник, все три стороны которого имеют одинаковую длину. Все его углы также равны между собой, и каждый из них равен 60-ти градусам. Отсюда ясно, что равносторонние треугольники всегда являются остроугольными.
Совет 2: Как определить тупоугольный и остроугольный треугольник
Простейший из многоугольников – это треугольник. Он образуется при помощи трех точек, лежащих в одной плоскости, но не лежащих на одной прямой, попарно соединенных отрезками. Тем не менее, треугольники бывают разных типов, а значит, обладают разными свойствами.
Инструкция
Принято выделять три типа : тупоугольные, остроугольные и прямоугольные. Это по типу углов. Тупоугольным называется треугольник, у которого один из углов является тупым. Тупым называется угол, имеющий величину больше девяноста градусов, но меньше ста восьмидесяти. Например, в треугольнике ABC угол ABC равен 65°, угол BCA равен 95°, угол CAB равен 20°. Углы ABC и CAB меньше 90°, но угол BCA больше, значит, треугольник тупоугольный.
Остроугольным называется треугольник, у которого все углы являются острыми. Острым называется угол, имеющий величину меньше девяноста и больше нуля градусов. Например, в треугольнике ABC угол ABC равен 60°, угол BCA равен 70°, угол CAB равен 50°. Все три угла меньше 90°, значит треугольник . Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.
Если в треугольнике один из углов равен девяноста градусам, это значит, что он не относится ни широкоугольному типу, ни к остроугольному. Это прямоугольный треугольник.
Если вид треугольника определять по соотношению сторон, они будут равносторонние, разносторонние и равнобедренные. В равностороннем треугольнике все стороны равны, а это, как вы выяснили, говорит о том, что треугольник остроугольный. Если у треугольника равны только две стороны или стороны не равны между собой, он может быть и тупоугольным, и прямоугольным, и остроугольным. Значит, в этих случаях необходимо вычислить или измерить углы и делать умозаключения, согласно пунктам 1, 2 или 3.
Видео по теме
Источники:
- тупоугольный треугольник
Равенство двух или более треугольников соответствует случаю, когда все стороны и углы данных треугольников равны. Однако существует ряд более простых критериев для доказательства данного равенства.

Вам понадобится
- Учебник по геометрии, лист бумаги, простой карандаш, транспортир, линейка.
Инструкция
Откройте учебник по геометрии седьмого класса на параграфе о признаках равенства треугольников. Вы увидите, что существует ряд основных признаков, доказывающих равенство двух треугольников. Если два треугольника, равенство которых проверяется, являются произвольными, то для них существует три основных признака равенства. Если же известна какая-то дополнительная информация о треугольниках, то основные три признака дополняются еще несколькими. Это относится, например, к случаю равенства прямоугольных треугольников.
Прочитайте первое правило о равенстве треугольников. Как известно, оно позволяет считать треугольники равными, если можно доказать, что какой-либо один угол и две прилегающие к нему стороны двух треугольников равны. Для того чтобы понять, данный закон, начертите на листе бумаги с помощью транспортира два одинаковых определенных угла, образованных двумя лучами, исходящими из одной точки. Отмерьте линейкой одинаковые стороны от вершины нарисованного угла в обоих случаях. Используя транспортир, измерьте величины полученных углов двух образованных треугольников, убедитесь, что они равны.
Для того чтобы не прибегать к таким практическим мерам для понимания признака равенства треугольников, прочитайте доказательство первого признака равенства. Дело в том, что каждое правило о равенстве треугольников имеет строгое теоретическое доказательство, просто его не удобно использовать в целях запоминания правил.
Прочитайте второй признак равенства треугольников. Он гласит, что два треугольника будут равны в том случае, если какая-либо одна сторона и два прилегающие к ней угла двух таких треугольников равны. Для того чтобы запомнить данное правило, представьте нарисованную сторону треугольника и два прилежащих к ней угла. Представьте, что длины сторон углов постепенно увеличиваются. В конце концов, они пересекутся, образуя третий угол. В данной мысленной задаче важным является то, что точка пересечения сторон, которые мысленно увеличиваются, а также полученный угол однозначно определяются третьей стороной и двумя прилегающими к ней углами.
Если вам не дана никакая информация об углах исследуемых треугольников, то используйте третий признак равенства треугольников. По данному правилу, два треугольника считаются равными, если все три стороны одно из них равны соответствующим трем сторонам другого. Таким образом, данное правило говорит о том, что длины сторон треугольника однозначно определяют все углы треугольника, а значит, они однозначно определяют и сам треугольник.
Видео по теме
Треугольник — это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника часто обозначаются маленькими буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
Остроугольным треугольником называется треугольник, у которого все три угла острые.
Тупоугольным треугольником называется треугольник, у которого один из углов тупой.
Прямоугольным треугольником называется треугольник, у которого один из углов прямой, то есть равен 90°; стороны a, b, образующие прямой угол, называются катетами ; сторона c, противоположная прямому углу, называется гипотенузой .
Равнобедренным треугольником называется треугольник, у которого две его стороны равны (a = c); эти равные стороны называются боковыми , третья сторона называется основанием треугольника .
Равносторонним треугольником называется треугольник, у которого все его стороны равны (a = b = c). Если в треугольнике не равна ни одна из его сторон (abc), то это неравносторонний треугольник .
Основные свойства треугольников
В любом треугольнике:
Признаки равенства треугольников
Треугольники равны, если у них соответственно равны:
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, если выполняется одно из следующих условий:
Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или её продолжение). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника .
Ортоцентр остроугольного треугольника расположен внутри треугольника, а ортоцентр тупоугольного треугольника — снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
Медиана — это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
Биссектриса — это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся центром вписанного круга. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.
Срединный перпендикуляр — это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга.
В остроугольном треугольнике эта точка лежит внутри треугольника, в тупоугольном — снаружи, в прямоугольном — в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Доказательство теоремы Пифагора
Построим квадрат AKMB, используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF, сторона которого равна a + b. Теперь ясно, что площадь квадрата CDEF равна (a + b) 2. С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB, то есть,
c 2 + 4 (ab / 2) = c 2 + 2 ab,
c 2 + 2 ab = (a + b) 2,
и окончательно имеем:
c 2 = a 2 + b 2 .
Соотношение сторон в произвольном треугольнике
В общем случае (для произвольного треугольника) имеем:
c 2 = a 2 + b 2 — 2 ab * cos C,
где С — угол между сторонами а и b.
- school-club.ru — какие бывают треугольники?
- math.ru — виды треугольников;
- raduga.rkc-74.ru — все о треугольниках для самых маленьких.
Треугольник - это многоугольник с 3-мя сторонами (либо 3-мя углами). Стороны треугольника нередко обозначаются малеханькими буквами, которые соответствуют большим буквам, обозначающим обратные вершины.
Остроугольным треугольником именуется треугольник, у которого все три угла острые.
Тупоугольным треугольником именуется треугольник, у которого один из углов тупой.
Прямоугольным треугольником именуется треугольник, у которого один из углов прямой, другими словами равен 90°; стороны a, b, образующие прямой угол, именуются катетами ; сторона c, обратная прямому углу, именуется гипотенузой .
Равнобедренным треугольником именуется треугольник, у которого две его стороны равны (a = c); эти равные стороны именуются боковыми , 3-я сторона именуется основанием треугольника .
Равносторонним треугольником именуется треугольник, у которого все его стороны равны (a = b = c). В том случае в треугольнике не равна ни одна из его сторон (abc), то это неравносторонний треугольник .
Главные характеристики треугольников
В любом треугольнике:
Признаки равенства треугольников
Треугольники равны, в том случае у их соответственно равны:
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, в том случае производится одно из последующих критерий:
Высота треугольника - это перпендикуляр, опущенный из хоть какой вершины на обратную сторону (либо её продолжение). Эта сторона именуется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке, именуемой ортоцентром треугольника .
Ортоцентр остроугольного треугольника размещен снутри треугольника, а ортоцентр тупоугольного треугольника - снаружи; ортоцентр прямоугольного треугольника совпадает с верхушкой прямого угла.
Медиана - это отрезок, соединяющий всякую верхушку треугольника с серединой обратной стороны. Три медианы треугольника пересекаются в одной точке, всегда лежащей снутри треугольника и являющейся его центром масс. Эта точка разделяет каждую медиану в отношении 2:1, считая от вершины.
Биссектриса - это отрезок биссектрисы угла от вершины до точки скрещения с обратной стороной. Три биссектрисы треугольника пересекаются в одной точке, всегда лежащей снутри треугольника и являющейся центром вписанного круга. Биссектриса разделяет обратную сторону на части, пропорциональные прилегающим сторонам.
Срединный перпендикуляр - это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга.
В остроугольном треугольнике эта точка лежит снутри треугольника, в тупоугольном - снаружи, в прямоугольном - посреди гипотенузы. Ортоцентр, центр масс, центр описанного и центр вписанного круга совпадают исключительно в равностороннем треугольнике.
Аксиома Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Подтверждение аксиомы Пифагора
Построим квадрат AKMB, используя гипотенузу AB как сторону. Потом продолжим стороны прямоугольного треугольника ABC так, чтоб получить квадрат CDEF, сторона которого равна a + b. Сейчас ясно, что площадь квадрата CDEF равна (a + b) 2. С иной стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB, другими словами,
c 2 + 4 (ab / 2) = c 2 + 2 ab,
c 2 + 2 ab = (a + b) 2,
и совсем имеем:
c 2 = a 2 + b 2 .
Соотношение сторон в случайном треугольнике
В общем случае (для случайного треугольника) имеем:
c 2 = a 2 + b 2 - 2 ab * cos C,
где С - угол меж сторонами а и b.
Дополнительно на сайт:





